
Faktor (Graphentheorie)

Ein Faktor ist in der Graphentheorie ein Teilgraph eines Graphen, bei dem gewisse Anforderungen an den Grad der Knoten sowie an den Zusammenhang des Graphen gestellt werden. Faktoren spielen eine wichtige Rolle in der Theorie des Matching-Problems und des Hamiltonkreisproblems.
Definition
Sei ein
einfacher Graph und
eine
Abbildung, die jedem Knoten des Graphen eine natürliche Zahl zuordnet.
Ein g-Faktor
ist dann ein
Teilgraph von
mit derselben Knotenmenge
wie
, in dem jeder Knoten
von
den Grad
besitzt, also genau
Nachbarn hat.
Gilt für alle Knoten
mit
die Bedingung
, besitzen also alle Knoten des Teilgraphen genau
Nachbarn, spricht man dementsprechend auch von einem a-Faktor.
Gilt dagegen für alle Knoten
die Bedingung
, besitzen also alle Knoten des Teilgraphen mindestens
und höchstens
Nachbarn, spricht man entsprechend von einem [a,b]-Faktor.
Äquivalente Definition
Äquivalent zur obigen Definition ist die folgende: Einen a-regulären Teilgraph, der den Graph
aufspannt, nennt man a-Faktor.
Verwandte Begriffe
Eine Zerlegung eines Graphen in a-Faktoren wird a-Faktorisierung genannt. Ein nichtleerer Graph heißt faktor-kritisch, wenn durch Wegnahme eines beliebigen Knotens eine 1-Faktorisierung möglich wird.
Beispiele
Eine Paarung ist ein
-Faktor, also ein Teilgraph von
, in dem jeder Knoten
höchstens einen Nachbarn hat. Eine
perfekte Paarung ist dagegen ein 1-Faktor, also ein Teilgraph von
, in dem jeder Knoten
genau einen Nachbarn besitzt.
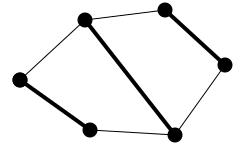
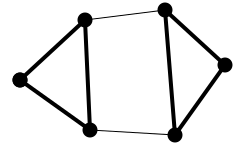
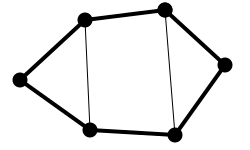
Hamiltonsche Graphen schließlich besitzen 2-Faktoren, in denen jeder Knoten
genau zwei Nachbarn hat.
Existenz von Faktoren
Der 1-Faktor-Satz von Tutte besagt, dass man aus
und
einen Graphen
konstruieren kann, welcher genau dann einen 1-Faktor besitzt, wenn
einen
-Faktor besitzt.
Dies ist die Definition einer Reduktion im Sinne der theoretischen Informatik. Da umgekehrt 1-Faktoren Spezialfälle von
-Faktoren sind, ist das
-Faktorproblem äquivalent zum 1-Faktorproblem.
Literatur
- Reinhard Diestel: Graphentheorie. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (354 S.).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.09. 2025